Tunneling of Sound
Imitation of quantum tunneling using acoustic waves
Imitation of quantum tunneling using acoustic waves
A new study of the Active Wave Control Lab from The Iby and Aladar Fleischman Faculty of Engineering shows for the first time that the quantum phenomenon "Klein tunneling", which describes a paradoxical passage of a particle through a potential barrier, can be accurately obtained in a classical system, such as sound wave propagation.
Tunneling is an abnormal and non-intuitive ability of particles/waves to cross gaps, barriers, or interfaces, although this crossing is forbidden in some sense for dynamic or energetic reasons. The realization of a classic analogy of this feature offers new and interesting capabilities in guiding waves in electromagnetic, acoustic, elastic systems and more. The study, led by Dr. Lea Beilkin-Sirota of the School of Mechanical Engineering, was recently published in the journal Physical Review Applied.
Imitation of quantum phenomena in classical systems - Is it possible?
The phenomena of quantum mechanics have their own laws, different from those familiar to us in classical systems, such as sound waves. But can we still "see" or "hear" a quantum phenomenon? It turns out that this is sometimes possible, thanks to the analogy that exists between the electronic band structure of materials and the acoustic frequency dispersion, for example. A notable example is the acoustic imitation of topological quantum phenomena, which allows the propagation of beam-like narrow sound waves that can also be unidirectional, as well as completely immune to reflection from corners, bends, and various structural defects. In this work we have tried to understand whether in a similar way there exists an exact analogy of the quantum tunneling phenomenon.
What is Klein tunneling?
The story begins with the Klein paradox, discovered by the renown physicist Oskar Klein about a century ago. This is a quantum phenomenon that predicts a perfect transmission of relativistic particles (moving at the speed of light) through an energy barrier that is higher than the energy of the particles. The paradox is that the particles can pass unimpededly through the barrier regardless of its height and width. Over the years an explanation for the paradox has been found, and the phenomenon has become a standard textbook exercise. However, the paradox returned to focus about 15 years ago, when the renowned physicists Andre Geim, Konstantin Novoselov and Mikhail Katsnelson showed that surprisingly, a similar phenomenon dubbed the Klein tunneling is supported by electron transfer in graphene (a single layer of carbon lattice) between two regions differing by an electrostatic potential. The principle of tunneling in graphene is based on the coupled two-component structure of its wave functions. It is this structure that allows the electron to move to the high potential region in a perfect transition without reflection in a normal incidence, and partial reflection in an oblique incidence.
Navigation of sound waves according to Klein tunneling laws
In our work we have shown that wave propagation similar to Klein tunneling can occur in classical systems, and surprisingly, even without relying on imitating the structure of graphene wave function and its corresponding dispersion relation. Instead, we proposed a mechanism that requires some form of parameters that define the medium (in the acoustic case these are the mass density and the bulk modulus), so that in the frequency range where the tunneling imitation takes place the parameters obtain negative values. In fact, the analogy of potential is the threshold between a 'positive' medium and a 'negative' medium. Such a medium does not exist in natural materials but can be obtained effectively using engineered materials (meta-materials). Such a medium is very popular in the study of meta-materials, as it allows for unconventional properties, such as negative refractive index, and more. Here, we demonstrated a direct relationship between the concept of the negative medium and a classical analogy of the Klein tunneling phenomenon, and we obtained transmission properties identical to the quantum properties. We illustrated this result using a two-dimensional tunneling of sound waves in an acoustic meta-material built from a periodic pattern of membranes and tubes that function as resonators. In addition, we have shown that by incorporating an anisotropy (property directionality) in the meta-material a perfect transmission for any incidence angle can be obtained, while retaining most of the original tunneling properties. We denoted the new phenomenon by "omnidirectional tunneling."
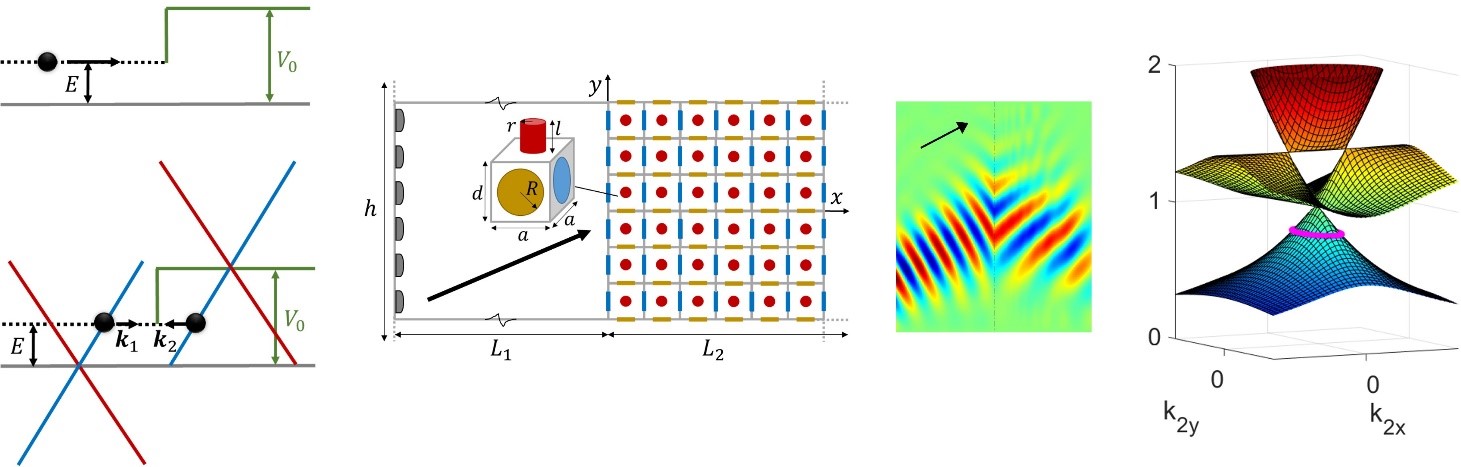
Acoustic analogue of Klein tunneling.
From left to right: A particle crossing a barrier, Klein tunneling in graphene, acoustic metamaterial imitating the classical analogue of the effect, dynamical response of the acoustic pressure field in the metamaterial, dispersion profile of the effective medium in the metamaterial
A little about us
In our group we explore how to obtain a medium with desirable properties of wave propagation dictated by the user, and adapt it to real-time changes in the operating conditions, such as variation in propagating wave frequency, in impedance, in boundary conditions, etc. We design control-based mechanical/acoustic meta-materials, in which external forces are applied to a simple basic structure (by implementing electronic transducers) according to the output of programmable controllers, based on measurements of the structure's response. This makes it possible to correct the structure's response in real time and adapt it to the changing environment. Our applications are wave guidance inspired by quantum phenomena, acoustic signature camouflage, creation of artificial acoustic environment, etc. We invite outstanding students to work with us and explore the fascinating world of wave propagation control.
For more details