Experimental and Theoretical Studies of Soliton-Soliton Collisions
Solitons (solitary waves) are self-trapped wave packets that keep their localized shape in the course of long-distance propagation, due to stable balance between linear spreading out, caused by diffraction and/or group-velocity dispersion, and nonlinear self-focusing. Solitons are fundamental collective-excitation modes in diverse areas, among which two most rapidly developing ones are nonlinear photonics and matter-wave optics (the latter pertains to coherent modes in atomic Bose-Einstein condensates (BEC)). Once the existence of individual solitons has been established, the next issue is collisions between them. Very often, solitons interact elastically, i.e., they pass through one another and emerge from the collision with original shapes, amplitudes, and velocities, the actual result of the collision being a shift of both solitons forward or backward, which seems as a discontinuous jump. This remarkable property is closely related to the fact that, in the simplest but relevant approximation, the soliton dynamics obeys integrable one-dimensional (1D) equations, such as the celebrated nonlinear Schrödinger equation (NLS), which emerges in the same form in a slew of different physical contexts. In particular, the NLS equation is the most fundamental model of both nonlinear photonics and atomic-wave optics. The integrability of the NLS equation implies that its solutions indeed produce elastic collisions between solitons.
The simple 1D approximation holds if the wave field is strongly confined in two transverse directions. Otherwise, in the three-dimensional (3D) setting, the integrability breaks down, the most dramatic consequence of that being a possibility of the collapse, i.e., catastrophic self-compression of the field. Accordingly, soliton-soliton collisions may exhibit complex outcomes, including the onset of collapse, merger of the colliding solitons into a single one, or the quasi-elastic rebound. The BEC in the gas of 7Li atoms makes it possible to realize both quasi-1D and fully 3D regimes, a crucially important experimental technique being the Feshbach resonance (FR), which makes it possible to control the strength of the self-attractive nonlinearity by means of an external magnetic field. While solitons were created in this setup more than 10 years ago [1,2], experimental and theoretical investigation of collisions between them was reported only very recently by Jason Nguyen, Paul Dyke, De Luo, Boris Malomed, and Randall Hulet, "Collisions of matter-wave solitons",
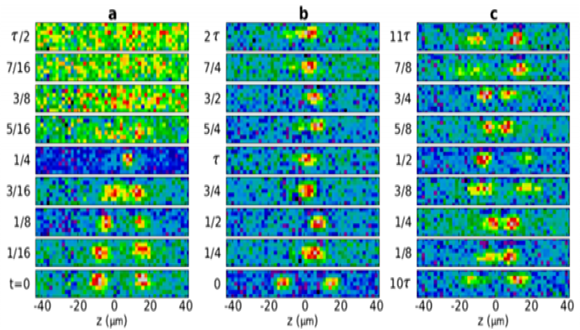
Nature Physics, DOI 10.1038/NPHYS3135, http://www.nature.com/nphys/journal/vaop/ncurrent/full/nphys3135.html (the work was supported by the Binational Science Foundation through grant No. 20110239). Using real-time in-situ imaging, it has been shown that the collision is a complex event, the outcome of which markedly depends on the relative phase between the colliding solitons. Adjusting the strength of the nonlinearity by means of the FR, the collisions have been examined in the proximity of the 1D - 3D crossover. All the above-mentioned outcomes were directly observed in the experiment, and explained theoretically by means of direct simulations and analytical consideration, which treats solitons as quasi-particles: the collapse, merger, and repeated rebounds (in the latter case, the solitons collide repeatedly as they are confined by a weak harmonic-oscillator trapping potential. These outcomes are shown, respectively, in images displayed in panels (a), (b), and (c) of the figure.
This work has quickly drawn attention of the major professional network, PhysicsWorld: http://physicsworld.com/cws/article/news/2014/nov/06/colliding-bose-einstein-condensates-vanish-from-sight.
[1] L. Khaykovich, F. Schreck, G. Ferrari, T. Bourdel, J. Cubizolles, L. D. Carr, Y. Castin, and C. Salomon, Formation of a matter-wave bright soliton, Science 296, 1290-1293 (2002).
[2] K. E. Strecker, G. B. Partridge, A. G. Truscott, and R. G. Hulet, Formation and propagation of matter-wave soliton trains, Nature 417, 150-153 (2002).